Skip to main content

Working Of Carnot Cycle And Its Process

 A  reversible cycle is an ideal hypothetical cycle in which all the processes constituting the cycle are reversible. Carnot cycle is the reversible cycle. For a stationary system, as in a piston and cylinder machine, the cycle consists of  the following four successive processes.




1. A reversible isothermal process in which heat Q1 enters the system at t1 reversibly from a constant temperature source at t1 when the cylinder cover is in contact with the diathermic cover A. The internal Energy of the system increases. 

From the first Law, 

Q1 = U2 - U1 + W(1-2) 

(for an ideal gas only, U1 = U2) 

2. A reversible Adiabiatic Process in which the diathermic cover A is replaced by the adiabiatic Cover B, and work We is done by the system adiabatically and reversibly at the expense of its inernal energy, and the temperature of  the system decreases from t1 to t2 . 

Using the first law , 

0 = U3 - U2 + W(2-3) 

3. A reversible isothermal process in which B is replaced by A and heat Q2 leaves the system at t2 to a constant temperature sink at t2 reversibly, and the internal energy of the system further decreases. 

from the first law, 

-Q2 = U4 - U3 - W(3-4)

only for an ideal gas, 

4. A reversible adiabatic process in which B again replaces A , and work Wp is done upon the system reversibly and adiabatically, and the internal energy of the system increases and the temperature rises from t2 to t1. 

Applying the first law, 

0 = U1 - U4 - W (4-1)

Two reversible isotherms and two reversible adiabatics constitute a Carnot cycle, which is represented in p-v coordinates 


      Q1 - Q2 = ( W(1-2) - W (2-3))  - ( W(3-4) + W(4-1) )

                          Q net = W net 

A cyclic heat engine operating under carnot cycle is called a Carnot Heat engine. 

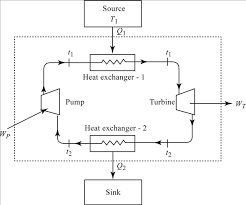
For a steady flow cycle ,






Labels:

Comments

Post a Comment

Popular posts from this blog

Advantages And Disadvantages Of Air Refrigeration System :

 Advantages Of  Air Refrigeration : 1. The refrigerant used namely air is cheap and easily available. 2. There is no danger of fire or toxic effects due to leakages. 3. The weight to ton of refrigeration ratio is less as compared to other systems. Disadvantages Of Air Refrigeration : 1. The quantity of  Refrigerant used per ton of refrigeration is high as compared to other systems. 2. The COP of the system is very low. Therefore running cost is high. 3. The danger of frosting at the expander valves is more as the air contains moisture content. 
Post a Comment
Read more

ELECTRICAL COMPARATORS AND ITS WORKING

Electrical Comparators are used as a means of  detecting and amplifying small movements of a work contacting elements. An electrical comparator consists essentially of  a pick-up head or transducer for converting a displacement into a corresponding change in current and a meter or recorder connected in the circuit to indicate the electrical change, calibrated to show in terms of displacement. Generally, an amplifier is needed to provide the requisite sensitivity and to match the characteristics of different parts of  the circuit. Electrical comparators can be classified according to the electrical principle used in the pick-up head. Most of the comparators use either a differential transformer, an inductance bridge, a strain gauge or a capacitor as a means of detecting movement of the gauging element. There are different types of  electrical comparators. One kind called an electrolimit gauge is used to check or measure the outside diameter of a  roll. The objec...
Post a Comment
Read more

SIMPLE CARBURETOR - CONSTRUCTION AND WORKING

CONSTRUCTION OF SIMPLE CARBURETOR :  The main Components of Simple Carburetor are : Float Chamber, float, nozzle, venturi, throttle valve, inlet valve, and metering jet . In the float chamber, a constant level of petrol is maintained by the float and a needle valve.  The float chamber is ventilated to atmosphere.  This is used to maintain atmospheric pressure inside the chamber. The float which is normally a metallic hollow cylinder rises and closes the inlet valve as the fuel level in the float chamber increases to certain level. The mixing chamber contains venturi, nozzle and throttle valve. The venturi tube is fitted with the inlet  manifold. This tube has a narrow opening called venturi. A nozzle is provided just below the centre of this venturi. The nozzle keeps the same level of petrol as that of the level in the float chamber. The mixing chamber has two butterfly valves.  One is to allow air into the mixing chamber known as choke valve. The other is to al...
Post a Comment
Read more